Problem-: Largest Rectangle in a Histogram
We have to find the largest area of a rectangle in a Histogram. we have given an Array of Integers representing a Histogram where the width of each bar is 1 Unit and height is the value of each index in the Histogram array. The largest rectangle in Histogram is that whose area is highest among all rectangles so formed.
Let us Understand how we can calculate largest area of rectangle in Histogram using Example.
Example 1 :
Your input
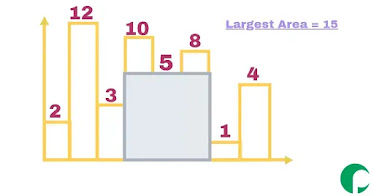
[2,12,3,10,5,8,1,4]
Output
15
Have a Look at Visualization Histogram
The basic Logic behind solving this problem is that we will get the largest triangle until we get an element lower than that element.
Also Read - [ Tower of Hanoi Problem ]
Brute force solution is the easiest way to understand this problem.
Brute force approach for Largest Triangle in Histogram.
class Solution {
public int largestRectangleArea(int[] heights) {
if(heights.length==1) return heights[0];
int area=0;
for(int i=0;i<heights.length;i++)
{
int min=Integer.MAX_VALUE;
for(int j=i;j<heights.length;j++)
{
min=Math.min(min,heights[j]);
area=Math.max(area,(j-i+1)*min);
}
}
return area;
}
}
After Going through the Brute force approach, you would understand the question and an approach to solve it.
As this Above solution will give TLE
Now let us Modify it to an efficient approach.
Solution of Largest Rectangle in a Histogram in Java
class Solution {
public int largestRectangleArea(int[] heights) {
if(heights.length==1) return heights[0];
Stack<Integer> st = new Stack();
st.add(0);
int i=0;
int area=0;
while(i<heights.length)
{
while(!st.isEmpty() && heights[i]<heights[st.peek()])
{
int t=st.peek();
int h= heights[t];
st.pop();
if(st.isEmpty())
{
area=Math.max(area,h*i);
}
else
{
int len=i-st.peek()-1;
area=Math.max(area,h*len);
}
}
st.add(i);
i++;
}
while(!st.isEmpty())
{
int t=st.peek();
int h= heights[t];
st.pop();
if(st.isEmpty())
{
area=Math.max(area,h*i);
}
else
{
int len=i-st.peek()-1;
area=Math.max(area,h*len);
}
}
return area;
}
}
Solution of Largest Rectangle in a Histogram in C++
int largestRectangleHistogram(vector<int>& height)
{
int n = height.size();
int max=0;
vector<int> left(n), right(n);
stack<int> st;
for(int i=0; i<n; i++)
{
if(st.empty())
{
left[i] = 0; st.push(i);
}
while(!st.empty() and height[st.top()] >= height[i])
st.pop();
left[i] = st.empty()?0:st.top()+1;
st.push(i);
}
while(!st.empty())
st.pop();
for(int i=n-1; i>=0; i--)
{
if(st.empty())
{
right[i] = n-1; st.push(i);
}
while(!st.empty() and height[st.top()] >= height[i])
st.pop();
right[i] = st.empty()?n-1:st.top()-1;
st.push(i);
}
for(int i=0; i<n; i++)
{
max = max(max, height[i]*(right[i]-left[i]+1));
}
return max;
}
};
The time complexity of the Largest Rectangle in the Histogram is O(n) if we use our stack approach.
Space Complexity of Largest Rectangle in Histogram is O(n).
The above solution is given by using Stack but You can use "Divide and conquer" algorithm to solve it more efficiently.
Solve this Problem at Leetcode
Leetcode problem Number 84 - Largest Rectangle in a Histogram










.png)